The Settlers of Catan (renamed to the shorter Catan, frustrating the abbreviation I had learned: Settlers) has dots on each of the number tokens. The rules state that "the larger the quantity of dots, the more likely it is that number will be rolled'' (5th edition rules). But how much more likely? The rulebook also lists the probabilities of rolling each number are as follows:
\begin{array}{ccc}
2 \,\&\, 12 &=& 3\% \\
3 \,\&\, 11 &=& 6\% \\
4 \,\&\, 10 &=& 8\% \\
5 \,\&\, 9 &=& 11\% \\
6 \,\&\, 8 &=& 14\% \\
7 &=& 17\%.
\end{array}
Are these correct? Yes and no. First, let's check to see if the probabilities add up to 100%. They don't; the sum is 101%. That means that either the numbers are wrong, or there's been some rounding and they aren't precise. The latter is the case here, which we'll see shortly.
Another indication that there's some rounding here is looking at the trend of the numbers. For results 2–7, the probability listed increases by 3% for each result, except when going from 3 to 4, which only increases by 2%. Could this be the case? In general, we could get such a weird almost pattern, but it's unlikely, and it's a flag that something else is going on. In this case though, we can say for certain that something is wrong here. When rolling 2d6 there are $6 \cdot 6 = 36$ possible outcomes. All events are a subset of these 36 outcomes. Thus, all probabilities must be an integer multiple of $1/36$, or
\begin{align}
p &= n \cdot \frac{1}{36}, \quad n \in \mathbb{Z}, \quad 0 \leq n \leq 36 \\
p &= n\cdot 0.02\overline{7}.
\end{align}
A couple notes on the notation: $\mathbb{Z}$ is the set of all integers and $0.02\overline{7} = 0.0277777777$ except with an infinite number of 7s. This explains the almost always increments of three percent, because the probability is in increments of $0.02\overline{7}$, when this gets rounded, it will most often get rounded up to an increment of $0.03 = 3%$. But every so often, we'll round down as the difference accumulates.
So what are the probabilities of each result of this 2d6 roll? We'll go through a few different ways to come up with it. First, the most brute force. As there are only 36 possible outcomes, it's not unreasonable to list them all out, which I've done for you in the following table.
\begin{array}{ccc}
\text{Sum} & \text{Die combinations} & \text{# combinations} \\
2 & 1\,\&\,1 & 1 \\
3 & 1\,\&\,2, 2\,\&\,1 & 2 \\
4 & 1\,\&\,3, 2\,\&\,2, 3\,\&\,1 & 3 \\
5 & 1\,\&\,4, 2\,\&\,3, 3\,\&\,2, 4\,\&\,1 & 4 \\
6 & 1\,\&\,5, 2\,\&\,4, 3\,\&\,3, 4\,\&\,2, 5\,\&\,1 & 5 \\
7 & 1\,\&\,6, 2\,\&\,5, 3\,\&\,4, 4\,\&\,3, 5\,\&\,2, 6\,\&\,1 & 6 \\
8 & 2\,\&\,6, 3\,\&\,5, 4\,\&\,4, 5\,\&\,3, 6\,\&\,2 & 5 \\
9 & 3\,\&\,6, 4\,\&\,5, 5\,\&\,4, 6\,\&\,3 & 4 \\
10 & 4\,\&\,6, 5\,\&\,5, 6\,\&\,4 & 3 \\
11 & 5\,\&\,6, 6\,\&\,5 & 2 \\
12 & 6\,\&\,6 & 1
\end{array}
For each sum I list all the different ways to get that sum, as well as a count of the number of combinations. Adding up all the counts shows that we have accounted for all 36 outcomes. For fair dice, each outcome is equally probable, so the probability of each sum is equal to the number of combinations divided by 36. These are listed in the table below, along with approximate decimal values as well as values rounded to the nearest percent. Note that the final column matches what the Settlers' rulebook lists as the probabilities.
\begin{array}{c|c|c|c}
\text{Sum} & \text{Probability} & \text{Approximate Probability} & \text{Probability to nearest percent} \\ \hline
2 & 1/36 & 0.0278 & 3\% \\
3 & 2/36 & 0.0556 & 6\% \\
4 & 3/36 & 0.0833 & 8\% \\
5 & 4/36 & 0.111 & 11\% \\
6 & 5/36 & 0.139 & 14\% \\
7 & 6/36 & 0.167 & 17\% \\
8 & 5/36 & 0.139 & 14\% \\
9 & 4/36 & 0.111 & 11\% \\
10 & 3/36 & 0.0833 & 8\% \\
11 & 2/36 & 0.0556 & 6\% \\
12 & 1/36 & 0.0278 & 3\%
\end{array}
It may be tempting to think that we've double counted some of the outcomes. For example, when the sum is 3 there are two combinations: 1 & 2 and 2 & 1. Aren't those the same? They have the same sum, but they're different cases, which is why I didn't write them as $1+2$ and $2+1$ (which are equivalent, due to the commutative property of addition: order doesn't matter). What we're saying is that it matters which die you roll the 2 on. Let's consider flipping a coin (or, a two-sided die) as a simple example to illustrate. Actually, let's first consider flipping two identical coins at the same time, but we'll identify one coin as the first coin, and the other as the second coin. Each coin can come up heads (H) or tails (T) with equal probability, and the results of each flip are independent (don't depend on each other). We can visualize the outcome space as a grid, plotting the possibilities of the first coin vertically, and the second horizontally, as shown below.
\begin{array}{cc|cc}
& & \text{Second coin} & \\
& & \text{H} & \text{T} \\ \hline
\text{First coin} & \text{H} & \text{HH} & \text{HT} \\
& \text{T} & \text{TH} & \text{TT} \\
\end{array}
Now, if you've studied the Monty Hall problem (this is pretty famous, so I probably won't take up space talking about it, unless I get into Monty Hall vs Deal or No Deal), or the woman in the park with two kids problem, you probably can see that TH (tails & heads) is different than HT. (This problem is less famous, but also much less game related.
C'est la guerre. But for the curious you may look here:
https://en.wikipedia.org/wiki/Boy_or_Girl_paradox. I find the notion of ambiguity related to this problem to be preposterous, due to the plain meaning of "at least one boy''. As referenced in the Wikipedia article, 17,946 readers of Marlyn vos Savant, perhaps unwittingly, agree with me.) However, to illustrate, let's say that the coins are different. Say we have a penny and a dime. Now our table looks a little more complicated.
\begin{array}{cc|cc}
& & \text{Dime} & \\
& & \text{H} & \text{T} \\ \hline
\text{Penny} & \text{H} & \text{PH, DH} & \text{PH, DT} \\
& \text{T} & \text{PT, DH} & \text{PT, DT} \\
\end{array}
Getting a heads on the penny and a tails on the dime is different than a heads on the dime and a tails on the penny. Still not seeing it?
Use 1d2 instead of a coin flip to keep better connected? Use blue and red dice. Then use one die with 1 and 2, and a second die with 3 and 4. Alternatively, just stick with coins and have one labeled arm and leg.
That was a fairly tedious and—more importantly—boring way of calculating the probabilities. Also, it only worked for our one case! What if we instead rolled 2d8 or 1d6+1d8? Let's try a more general technique.
To start, let's still only look at two dice, but let's compute the probabilities in a way that that's more efficient. Say we roll 1d$N$ + 1d$M$. In this case there are $N \cdot M$ total outcomes. The total will range from $2$ to $N+M$. We can gain follow the same approach of counting the number of ways to get each result. So the probability of getting a total result $x$ is,
\begin{align}
P(x) = \frac{(\text{# ways to get }x) }{N \cdot M}.
\end{align}
So the problem again boils down to counting the number of ways to get $x$. When the total is $x$, there are a total of $x$ pips (the dots) on both dice (let's just assume these are dice with pips, as it makes the explanation easier). Each die must have at least 1 pip. The first die can have a maximum of $N$ pips, and the second $M$ pips. Under such a constraint, how many different ways can you sum to $x$? If we draw a picture it becomes a little easier.
Let's consider the case of $x=6$ when rolling 2d6. Let's spread out these 6 pips in a row, as shown below.
*
*
*
*
*
*
Now, we'll represent how many pips are on which die by putting a line somewhere in the middle. So if we have 2 on the first die, and 4 on the second die, we can draw it like this:
*
*
|
*
*
*
*
Because need at least one pip on each die, we have as many ways of dividing the pips as there are interior spaces between the pips in the drawing. I've highlighted all possible divisions below:
*
|
*
|
*
|
*
|
*
|
*
It's pretty clear that in this case, the number of combinations is equal to the number of pips minus 1, or $x-1$. This is equivalent to the number of ways to roll $x$. Thus,
\begin{equation}
P(x) = \frac{x-1}{N \cdot M}.
\end{equation}
But the above example doesn't cover all cases. We didn't have to invoke the fact that we can have at most $N$ pips on the first die, and $M$ pips on the second die. So this really only works when $x$ is less than or equal to the minimum of $N$ and $M$. Without loss of generality, we can assume that $N$ is less than or equal to $M$. (This is because it doesn't matter which number we assign to $N$ as opposed to $M$. That is, if we have 1d6 and 1d8, we can assign 6 and 8 to $N$ and $M$ as we please. It doesn't change the nature of the two dice.) So,
\begin{equation}
P(x) = \frac{x-1}{N \cdot M}, \quad x \leq N \leq M.
\end{equation}
We can see that this agrees with our table for the 2d6 case.
Now let's consider a large case, when $x$ is larger than $M$. Here we must constrain that there are at most $N$ pips on the left, and $M$ pips on the right. Let's continue with the 2d6 example and look at $x=9$.
*
*
*
*
*
*
*
*
*
There are still $x-1$ interior spaces, but not all of them are valid. Instead, we must consider only the leftmost 6 spaces to ensure that the left die has at most 6 space, shown here:
*
|
*
|
*
|
*
|
*
|
*
|
*
*
*
Similarly, we must also only consider the
right most 6 spaces to ensure that the
right die has at most 6 space, shown here:
*
*
*
|
*
|
*
|
*
|
*
|
*
|
*
The overlap of these two restrictions shows the number of ways to get a total of 10 here:
*
*
*
|
*
|
*
|
*
|
*
*
*
In this case, we can see there are 4 ways, which matches our previous table. But how can we express this in general, especially in terms of $N$ and $M$? Let's number the dividing positions as follows.
*
1
*
2
*
3
*
4
*
5
*
6
*
7
*
8
*
The restriction on the left die limits us to use positions 6 and less, or $N$ and less in general. The restriction on the right die limits us to use positions 3 or more. But where does the 3 come from? It's 6 positions counting from the right. $3=9-6$. So in general, we're limited to position $x-M$ and more. The number of positions from $x-M$ to $N$ (inclusive) is $N$ minus $x-M$ plus 1. So,
\begin{align}
P(x) &= \frac{N - (x-M) + 1}{N \cdot M} \\
P(x) &= \frac{N+M - (x-1)}{N \cdot M},\quad x \geq M \geq N.
\end{align}
Does the plus 1 not make sense? In our example $6-3=3$ covers the numbers 4–6, while the $+1$ covers position 3 itself.
That covers all the cases we saw in our 2d6 roll, and matches up with our table. But what about the case when $x$ is between $N$ and $M$ ($N < x < M$), when $N$ and $M$ are different ($N \neq M$)? Let consider 1d4+1d8 with $x=6$.
We're restricted to the the left four dividing locations by the d4:
*
|
*
|
*
|
*
|
*
*
Here we're not limited by the maximum of the d8, only the minimum, but that restriction is redundant with the d4 maximum restriction. Thus, the number of divisions is simply $N$. So the probability is,
\begin{align}
P(x) &= \frac{N}{N \cdot M} \\
P(x) &= \frac{1}{M}, \quad & N < x < M .
\end{align}
To put everything together,
\begin{align}
P(x) &= \frac{x-1}{N \cdot M}, & x \leq N \leq M \\
P(x) &= \frac{1}{M}, & N < x < M \\
P(x) &= \frac{N+M - (x-1)}{N \cdot M},& N \leq M \leq x.
\end{align}
Note that the first and third equations do match our previous results when $x=N=M$. This is a good check to do to help ensure we didn't make any mistakes. It doesn't guarantee that we didn't, but it helps build confidence.
So now we know the probability of any total result when rolling two dice of any type or combination of types. But what about three or more dice? We might be able to extend the above analysis method to three dice, but it's going to get tedious, and probably difficult. And honestly, we'd probably make a mistake. Let's take a detour and look at some other aspects of this, and then we'll come back to do some more generalizing.
One of the things that's striking when looking at the table of probabilities is the symmetry. The probability steadily increases from 2 to 7, and then decreases correspondingly from 7 to 12. In fact, the probability of getting a number $y$ away from 7 is the same whether the number is $7+y$ or $7-y$. That is,
\begin{align}
P(7-y) = P(7+y) .
\end{align}
Or we could think of the symmetry from the ``outside''. The probability of getting 2 is the same is 12, 3 the same as 11, or in general,
\begin{align}
P(x) = P(14-x).
\end{align}
Is this some happy accident, or should we expect this? We should expect this, and in fact, we should have used it to our advantage when calculating the probabilities in the first place (I didn't for your benefit). Calculating the probabilities for $x > M$ was even more cumbersome. We could have saved some real work. First, let's confirm that this falls out from our equations. For $N=M=6$, we have:
\begin{align}
P(x) &= \frac{x-1}{36}, & x \leq 7 \\
P(x) &= \frac{13 - x}{36}, & 7 \leq x. \label{eq:2d6_2}
\end{align}
If $x \leq 7$, then $14-x \geq 7$. You can do this step by step as follows. Assuming $x \leq 7$, we then multiply both sides by $-1$ and then add $14$ to both sides.
\begin{align}
x & \leq 7 \\
-x & \geq -7 \ \\
14 - x & \geq 14 - 7 = 7.
\end{align}
Note: multiplying by $-1$ switches the direction of the inequality.
Thus, to evaluate $P(14-x)$, we use an equation for $P(x)$ when $7 \leq x$ from above. Evaluating that, we find that,
\begin{align}
P(14-x) = \frac{13 - (14-x)}{36} = \frac{x-1}{36} = P(x) \quad \blacksquare
\end{align}
Here the $\blacksquare$, is a symbol meaning QED, which short for the latin
quod erat demonstrandum, meaning roughly: that which was to be proven. It's how we end a proof and say we're done. The way most proofs are structured it's usually anticlimactic, as you prove some small piece that you had earlier assumed you could prove to make the bigger point.
I'll try to be a little less anticlimactic. Does this make sense intuitively? I'll claim yes, but if you haven't thought about it I can understand why you might not think so yet. Let me try to explain what I'm thinking. Let's think about the minimum and maximum cases here. Let's stick to 2d6 to be concrete. The one way to get the minimum—2—is to roll the minimum on each die. Similarly, the way to get the maximum—12—is to roll the maximum on each die. That's symmetry. In fact, you can extend this all the way down. Let's say we take a marker and relabel all the sides of the dice as follows,
\begin{align}
1 & \rightarrow 6\\
2 & \rightarrow 5\\
3 & \rightarrow 4\\
4 & \rightarrow 3\\
5 & \rightarrow 2\\
6 & \rightarrow 1.
\end{align}
Or,
\begin{align}
x_1 &\rightarrow 7 - x_1 \\
x_2 &\rightarrow 7 - x_2 .
\end{align}
Where $x_1$ is the result of the first die and $x_2$ is the result of the second die. With the sum $x$,
\begin{align}
x = x_1 + x_2
\end{align}
Thus, our relabeling is equivalent to
\begin{align}
x \rightarrow (7-x_1) + (7-x_2) = 14 - x_1 - x_2 = 14 - (x_1+x_2) = 14-x.
\end{align}
Since we can relabel the dice such that a result $x$ becomes $14-x$, the probability of those two events must be equal. Actually, we're also assuming that the probability doesn't change when we do the remapping. That is,
\begin{align}
P(x_1) = P(7-x_1).
\end{align}
This is true, because we roll each of the faces of a die with equal probability (I'm assuming fair dice here).
\begin{align}
P(x_1) = \frac{1}{6} \quad x_1 \in \{1, 2, 3, 4, 5, 6\}
\end{align}
Since this assumption is true, then we can conclude that yes, in general,
\begin{align}
P(x) = P(14-x).
\end{align}
I'll leave it as an exercise for the reader to prove the general case of 1d$N$ + 1d$M$. But note that this explanation—and derivation really—are more robust than the first one that we did. At first, we just took the equations that we had derived that showed that in this case they worked out to be symmetric about the middle value of 7. In this case though, we've proved that the symmetry in the probability of the sum exists due to the symmetric property of the individual dice (that the faces have equal probability).
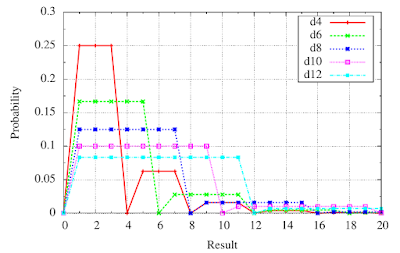
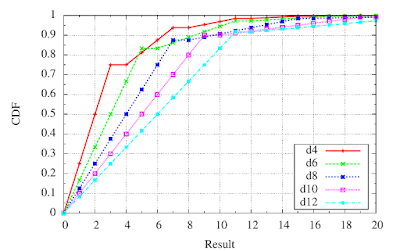
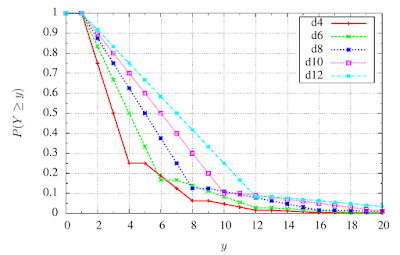
For 11 possible sums, listing the probabilities is manageable, albeit somewhat tedious. The same information is often displayed graphically. First, let's simply plot the probabilities in the table above.
 |
| Probability mass function (pmf) of 2d6 |
This plot shows the probability mass function (pmf) of the random variable given by the sum of rolling 2d6. On the plot we can see the probability increase linearly form 2 to 7, where it peaks, and then decrease from 7 to 12.